Python으로 Neural Net 체험하기 (0): 단층 신경망 최적화

Machine Leraning이나 Neural Net에 대해서는, 한국어로도 잘 설명된 블로그 글이나 유튜브 영상이 범람 상태입니다. 이 글에서는 설명을 생략합니다. 

 

다만, 제가 관련 개념을 잡을 때 재미있게 보았던 링크를 하단과 같이 첨부합니다. 아래 글과 영상만 보셔도 대략의 감을 잡는데 도움이 될 것입니다.

수아랩 블로그  

But What is a Nerual Network? (영어 자막 있음) 

 

0. 이 글의 목적 

Single Layer Neural Network의 최적화에 활용되는 Delta Rule을 python code를 통해 직접 구현해봅니다. 

아래 코드들은 사실 keras나 pytorch같은 딥러닝 프레임워크에서 옵티마이저로 한 줄이면 구현 가능한 것들입니다.

하지만... 전자계산기 대신 직접 손으로 계산 과정을 써가면서 공부하면 머릿속에 유도 과정 같은 것들이 더 잘 남고 그렇지 않습니까? 비슷한 맥락에서 Neural Network이 직접 돌아가는 원리를 더 잘 알고자 직접 코드를 짜보았습니다.

 

1. 이 글에서 알고자 하는 사항

- [0,0,1],[0,1,1],[1,0,1],[1,1,1]의 입력에 대해 0,0,1,1의 정답을 출력할 수 있는 인공 신경망을 학습시킨다. (지도학습)

- SGD(Stochastic Gradient Descent), Batch, Mini Batch를 모두 구현한 다음, 어떤 방법이 가장 효율적인 학습 방법인지 알아본다.

 

2. 개념 설명

0) Single Layer Neural Network

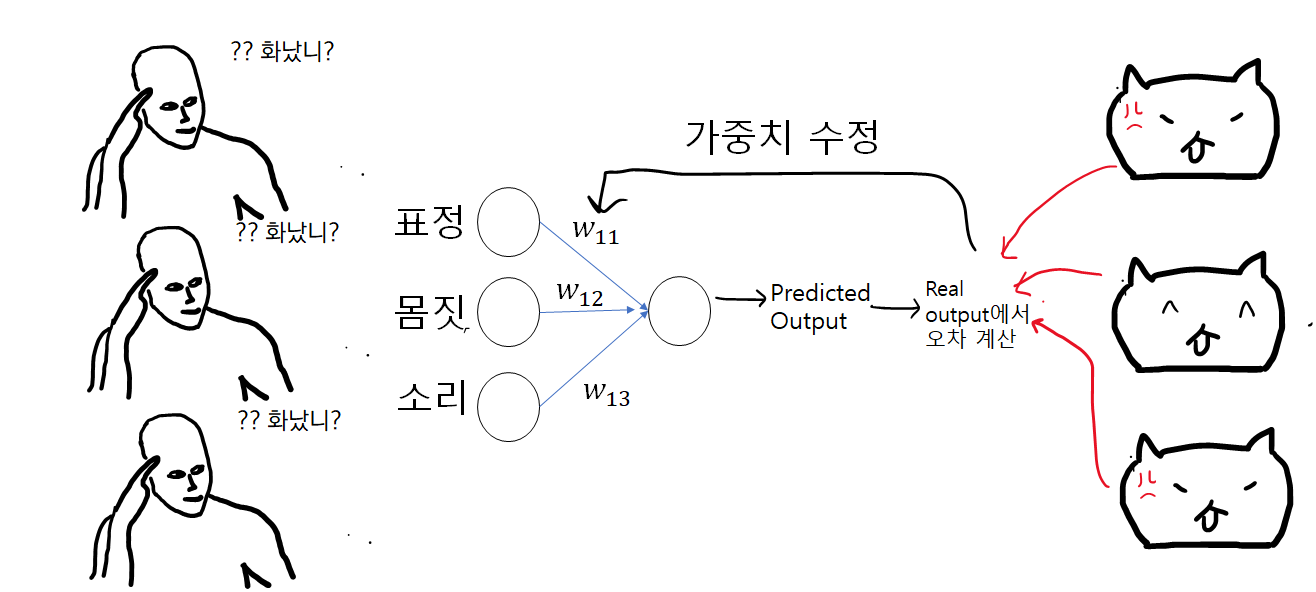
rough한 비유로 먼저 시작해 보겠습니다. 제가 고양이와 대화를 할 수 있게 되어, 고양이가 화났는지(1) 안 화났는지(0) 알려줄 수 있다고 합시다. 이를 "Angry Cat Prediction Algorithm"이라 지금부터 명명하겠습니다.

위와 같이 고양이가 화났는지 화나지 않았는지 판별할 수 있는 인공지능은 하늘에서 뚝 떨어지지 않습니다.

우선 어떤 요인에 의해 고양이가 화났는지를 판단할 수 있는지 정해주어야겠죠. 표정, 몸짓, 소리 정도를 input data로 두겠습니다.

그 다음엔 표정, 몸짓, 소리 각각에 대한 weight가 있어야 될 것이고, 그 weights를 바탕으로 화났는지 화나지 않았는지 판단을 할 것입니다. 이 판단이 제대로 되었는지 알려줄 expected output data 필요하구요. 위의 과정을 그림과 같이 정리했습니다.

위의 상황에서는 입력*가중치(weight)=출력의 단순한 구조를 거쳐 고양이가 화났는지를 판단했는데요. 이와 같이 입력-출력의 단순한 Neural Net 구조를 Single Layer Nerual Network라 합니다.

 

1) Delta Rule 

위의 과정에서 고양이가 알려준 정답을 바탕으로 weight를 수정하는 과정이 있었는데요. 이 weight를 수정하는 구체적인 방법이 Delta Rule입니다.

원시적인 수준의 Delta Rule은 다음과 같습니다.

(alpha: learning rate, e_i: error, x_j: input value)

그런데 위와 같이 학습하는 경우, 다양한 문제가 발생합니다. 예컨대, learning rate가 높은 숫자일 때, weight이 적절한 정답을 줄 수 있는 값에 수렴해 가지 않는 경우가 발생합니다. 위의 수식에서 learning rate와 input value는 상수이므로 새로운 weight에서 error가 감소해야 하는데, 오히려 새로운 weight이 error를 증가시켜 버렸다면 오차가 증가하는 방향으로 쭉 발산해 버리는 것이지요. 이해가 잘 가지 않는다면, 아래와 같이 개선된 Delta Rule이 존재한다는 것만 알아도 충분합니다.

위의 Delta Rule에서 이상한 도함수가 추가되었습니다. 이 함수는 Sigmoid Function의 도함수로서, sigmoid function이 무엇인지는 이 영상을 참고하길 바랍니다: But What is a Nerual Network? (영어 자막 있음)

 

3. 실제 구현

이제 위의 학습 규칙을 실제 학습에 적용해보겠습니다.

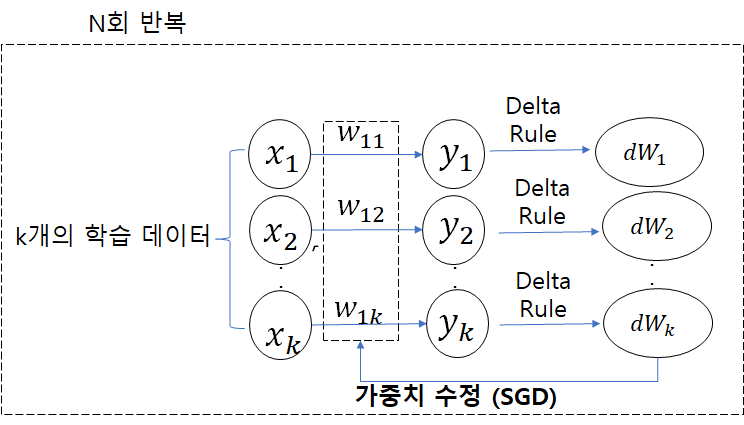
• SGD는 한개의 학습 데이터마다 매번 오차를 계산해 weight를 갱신하는 방식입니다.
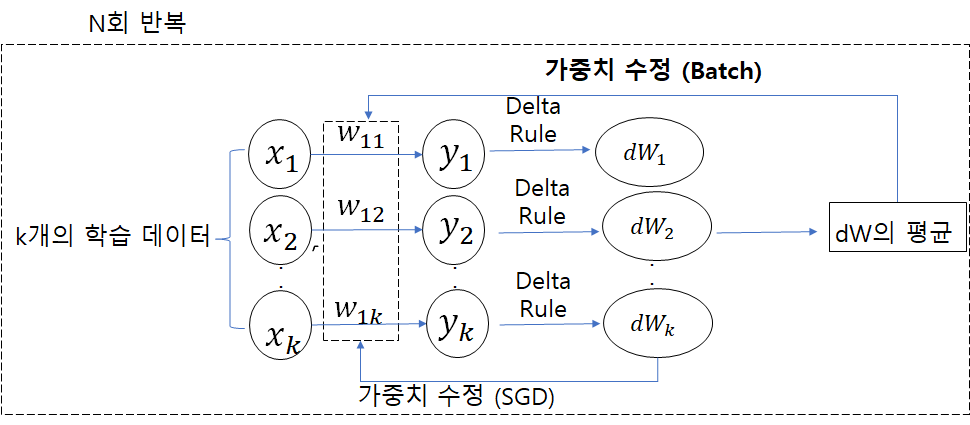
• Batch는 모든 학습 데이터에 대해 오차의 weight 갱신값을 모두 구한 후, 이를 바로 취하지 않고 평균값을 모든 weight 갱신에 활용하는 방식입니다.
• Mini-Batch는  Batch와 달리 모든 학습 데이터를 활용하지 않고 일부만 활용하여, 이들의 평균으로 weight을 갱신하는 방식입니다.
• 자세한 개념 설명은 이 블로그 혹은 이 블로그를 참고하세요.

0) 시그모이드 함수 정의

우선 모든 함수는 패키지에 저장해두도록 하겠습니다. 오늘 sigmoid function의 input은 스칼라밖에 없지만, multi-layer neural net부터는 array를 받는 경우도 생겨 조건문으로 세팅해두었습니다.

def sigmoid(x):
    if type(x)==float or int:
        z = 1 / (1 + np.exp(-x))
        return z
    if type(x)==np.array:
        z=[]
        for i in x:
            y = 1 / (1 + np.exp(-i))
            z.append(y)
        return z

package/onelayer.py

def deltabatch(W,X,D,T):
    for i in range(T):
        alpha=0.9
        dWsum=np.zeros(3)
        N=4
        for k in range(N):
            x1 = X[k]
            d = D[k]
            v=np.dot(W,np.transpose(x1))
            y=sigmoid(v)
            e=d-y
            delta=y*(1-y)*e
            dW = alpha * delta * x1
            dWsum = dWsum+dW
        dWavg = dWsum / N
        for i in range(3):
            W[0,i]+=dWavg[0,i]
 
    return W

3) Mini Batch 실행

사실 저희는 입력 데이터가 4개밖에 없어서 Mini Batch를 쓰기가 뭣하긴 합니다만...

Batch처럼 평균을 내도록 하되, 지정된 Batch Size (주로 2의 거듭제곱)만큼에서만 평균을 내 가중치 갱신에 활용하는 방식입니다.

예컨대, 문제 상황의 4개의 학습 데이터([0,0,1],[0,1,1],[1,0,1],[1,1,1]) 중 2개의 데이터를 묶어, 이 2개의 데이터에 대해서만 Batch 방식처럼 weight의 평균을 반영해 weight을 갱신할 수 있는데, 이 행위를 2번 실행하면 (2*2=4) 전체 데이터에 대한 학습을 완료할 수 있습니다. 이를 Mini Batch방식이라 합니다. 

실제 구현 사례에서 batch_size라는 변수가 추가되어, 일부 학습 데이터에 대해서만 가중치 갱신을 하는 것을 보실 수 있습니다.

package/onelayer.py

def deltaminibatch (W,X,D,T):
    for i in range(T):
        alpha=0.9
        dWsum=np.zeros(3)
        N=4
        batch_size=2
        a=int(N/batch_size)
        for i in range(batch_size):
            for k in range(a):
'''
위의 부분이 mini batch를 위해 추가된 부분으로, 2(N/batch_size)개의 입력 데이터에 대해
2회 (batch_size) 학습을 진행해 총 N개의 입력 데이터에 대한 학습을 완료했습니다.
'''
                x1 = X[k+batch_size*i]
                d = D[k+batch_size*i]
                v=np.dot(W,np.transpose(x1))
                y=sigmoid(v)
                e=d-y
                delta=y*(1-y)*e
                dW = alpha * delta * x1
                dWsum = dWsum+dW
            dWavg = dWsum / a
            for j in range(3):
                W[0,j]+=dWavg[j]
 
    return W

from sympy import *
from random import *
import numpy as np
import time
import math
from pkg.onelayer import deltaminibatch
from pkg.functions import sigmoid
 
X=[[0,0,1],[0,1,1],[1,0,1],[1,1,1]]
D=[0,0,1,1]
 
W = np.random.uniform(low=-1.0,high=1.0, size=(1, 3))
deltaminibatch(W,X,D,10000)
for i in range(4):
    x1 = X[i]
    v = np.dot(W,np.transpose(x1))
    y = sigmoid(v)
    print(y)
 

더욱 작은 표본의 평균을 구한다는 점을 제외하면, batch 방식의 그것과 매우 닮았습니다. 그러나 결과는 batch방식보다 훨씬 우월했습니다. 결과는 다음과 같습니다:

[0.01021221]
[0.00830992]
[0.99039899]
[0.98820465]

실행시간 3.09초

 

4. XOR 문제

한편, 위 학습 데이터에서(입력: [[0,0,1],[0,1,1],[1,0,1],[1,1,1]] 출력:[0,0,1,1]) 출력값을 [0,1,1,0]로 바꾸면 알고리즘은 [0,1,1,1]에 가까운 답을 내놓습니다. 이는 바뀐 학습 데이터가 linearly seperable하지 않기 때문입니다.

입력 데이터를 기하와 벡터에 나오는 공간좌표 상의 한 점이라고 생각합시다. ([x축, y축, z축])

위 입력 데이터는 모두 z=1상에 있는 점들이고, 다음과 같이 표현될 수 있습니다.

어느 직선으로 평면을 잘라도 출력 0과 1을 구분하는 역할을 할 수가 없습니다. 이를 linearly seperable하지 않다고 합니다. (출처: https://medium.com/@jayeshbahire/the-xor-problem-in-neural-networks-50006411840b)

반면, 오늘 다루었던 학습 데이터는 다음 그림과 같이 출력 0과 1을 구분하는 기능을 하는 직선이 있습니다. 즉, linearly seperable하여 높은 정확도로 정답을 예측할 수 있었습니다.

 

이 글에서 다루었던 single layer neural net은 결국 A*x+b 꼴로 생긴 선형방정식이기 때문에, linearly seperable하지 않은 학습 데이터에 대해 제대로 된 정답을 내놓을 수 없는 것입니다. 이 문제를 XOR문제라 하며, 이를 해결하기 위해 더 많은 layer를 가진 multi layer neural net이 필요합니다.

 

Multi Layer Neural Net의 학습에 관해서는, 다음 포스트에서 좀 더 자세히 배워보도록 하겠습니다.

 

5. Reference

예제와 기본 구현 알고리즘은 김성필, "딥러닝 첫걸음" 한빛미디어를 참고하였다.